NET PRESENT VALUE
The concept is used widely by professionals for valuing liabilities and monetary assets. It is also used as a useful tool for evaluating proposals related to long term investmets like purchase of fixed assets etc.
1. FINDING PRESENT VALUE
The Present Value (PV) of an amount p, discounted at a rate i for n years, is given by –
The Present Value (PV) of $100 discounted at 5% interest rate for 20 years is given by –
2. FINDING PRESENT VALUE FOR A SERIES OF PAYMENTS
Most of the investments result in a series of future cash inflows over a period of time rather than providing one time returns. In such scenarios, present value for each of these individual cash inflows is added to calculate the present value for the series of payments.
Note. For computational purposes, we assume that each of these individual payments is earned & received at the end of the period rather than continuously throughout the period.
Example. Calculate the present value for the following series of payments at 10% discount rate: year 1, $5000; year 2, $7500; year 3, $3000; year 4, $500?
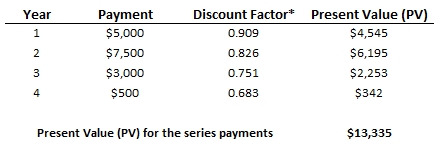
For the above computation, Discount factor for each year is calculated as the PV of $1 received in each year; and is later multiplied by the original payment amount to calculate the PV of the payment. This is done only to simplify calculations.

Many business investments often result in a series of periodic & equal amounts of cash inflows. Technically, such a series of equal payments are termed as annuity. E.g. repayment of loans
3. NET PRESENT VALUE (NPV)
Net Present Value (NPV) is often an important metric to look at, while evaluating corporate projects for a “Go No-Go” decision. Any corporate project would typically require an investment to build some capability which later it tries to leverage and gain additional cash inflows for the organization.
The difference between the initial investment and the present value of the future cash inflows spread over the useful life of the investment is termed as Net Present Value.
THE INVESTMENT PROPOSAL IS ACCEPTABLE, IF NPV IS GREATER THAN ZERO
Example. An organization is evaluating an investment opportunity where $50,000 of initial investment is expected to generate cash inflows of $35,000 per year for the next 2 years. Should they go-ahead with this investment?
The present value of the future cash inflows can be calculated as follows. Net Present value is then derived from it by deducting the initial investment.

The proposed investment is acceptable as the NPV of the proposal has turned out to be greater than zero.

Calculating NPV for a long-lived asset or any business proposal looks fairly simple and formula based. But, it isn’t entirely true. The challenge is here not in calculating NPV but estimating the input variables required to calculate NPV. As you must have already noticed, NPV for any asset or business proposal is dependent on following factors –
- Discount rate
- Initial investment
- Useful life for an asset or business proposal
- Cash flow each year
- Terminal value
The value of these variables will vary from business to business or from one asset to another. Therefore, it is important to understand how these values are to be derived in order to get best possible NPV value for proposals. Following section talks how these terms are interpreted in the business domain and about the methodologies that are adopted to derive their values.
4. ESTIMATING THE VARIABLES
Capital investment calculations using NPV methodology requires one to estimate following five elements first –
- Discount rate (or, Required rate of return)
- Useful life (# of years for which cash inflows are anticipated)
- Expected cash inflow & outflow in each year
- Amount of Initial Investment
- Terminal Value
Below section discussed the relevance of these elements and the basis on which these can be estimated for NPV calculations.
4.1 DISCOUNT RATE (OR REQUIRED RATE OF RETURN)
Discount rate can be derived using two alternate ways – trail & error and cost of capital. Each of these methods is described below –
4.1.1 TRIAL AND ERROR
We have already seen, that discount rate is inversely proportional to NPV, i.e. if the discount rate selected is higher; NPV will be lower; resulting in lesser projects reaching approval bucket of senior management.
To start with, a company may select a discount rate that’s prevailing in the industry and adopted by other players in the same domain. Now this may result in two possible scenarios, at the assumed discount rate either the management will be flooded with the business proposal or there would be a very high rejection of projects at the early stage itself. Former scenario indicates the assumed discount rate was too low and thus must be increased. In the later scenario, it must be decreased to allow further discussion on higher number of proposals.
4.1.2 COST OF CAPITAL
Ideally, the discount rate (or the required rate of return) should be equal to the organizations’ cost of capital. Since, organizations raise capital in form of debt & equity; Cost of capital is defined as the weighted average for the cost of debt & the cost of equity invested in the organization as per its capital structure.
Example. An organization has raised $1 million for funding their future projects. $300k of it was raised through debt and remaining $700k via equity. What could possibly be organization’s Cost of Capital? (Assume cost of raising debt capital is 5% and that of equity at 15%)
The Cost of capital for the organization can be calculated as follows –
Cost of Capital (Debt) = 5%; Weight = 30% (As 30% (300k) of the total amount is raised through debt)
Cost of Capital (Stocks) = 15%; Weight = 70% (As 70% (700k) of the total amount is raised through equity)
Cost of Capital = 5%*0.3 + 15%*0.7 = 12%
Calculating cost of equity element present in above formula often becomes a challenge for most of the companies. Cost of equity is defined as the rate of return that equity investors are expecting from their investment in the company. Since it is just an expected rate of return for investors, most of the companies do not get into detailed numerical analysis for deriving it; rather they opt for a judgmental approach for assuming it.
It is important to understand the cost of capital thus calculated is applicable for proposals with average risk involved. In case the risk associated with a proposal is higher; a higher cost of capital must be used for evaluating such proposals. Contrary, lower required rate of return can be used for evaluating proposal with below-average risk profiles.
4.1.3 EFFECT OF NON-DISCRETIONARY PROJECTS ON COST OF CAPITAL
Most of the companies are often required to execute projects that are non-capital in nature. Projects like implementing environmental safety, improving work conditions, creating recreational facilities etc fall under this category. Such projects are called necessity projects or non–discretionary projects. Although no cash inflow is expected from these projects but they do require capital investments.
Therefore to fund these necessity projects, it becomes important for a company to use a discount rate that is higher than cost of capital for evaluating discretionary projects.
4.2 USEFUL LIFE
The useful life of an investment is estimated to be the number of years over which earnings from the project can be expected. Although someone may argue that most of the projects may provide cash inflows for indefinitely long periods; but for practical purposes, we assume the economic life of an investment to be 5, 10, 15 or 20 years. The rationale behind this approach is mainly the uncertainty involved in predicting cash inflows over longer periods.
Also, the present value of future earnings for distant years is so less that its contribution can simply be avoided e.g. at a discounted rate of 15%, the cash inflow of $1 in the year 25 has a present value of 3 cents.
4.3 CASH INFLOWS
Cash inflows are the differential earnings resulting from the investment made versus when no investment is made.
A simple example to demonstrate that could be a purchase of equipment. The investment in this new equipment will either lower down the operating costs(thus reducing operating expenses) or increase the volumes of goods produced (thus resulting in additional revenue). Monetary benefits related both of these, must be calculated and compared to operating costs & revenues associated with the current equipment in use. This differential when extrapolated for future years will result in cash flows related to this investment.
There might be business scenarios, where cash inflows from the investment on new equipment might not turn out to be significant; but still company may choose to go ahead with the investment; as not doing so might result in an advantage for the competitor.
4.4 INVESTMENT
The amount of funds, an entity risks in accepting a proposal is termed as investment. E.g. in the purchase of an asset; the cost of purchase, installation, shipping, training etc are all considered a part of investment.
4.5 TERMINAL VALUE
Terminal value of an investment is defined as the fair value of the assets (created via investment) at the time of its disposal. Time of disposal for an asset is often marked at the end of its useful life. Present value of this amount is calculated as cash inflow for NPV calculations.
Example. Suppose an organization decides to replace & sell off existing equipment at the end of its useful life of 5 years. The company gets $5,000 from the proceeds of its sale.
In this case, $5,000 will be considered as the terminal value for this asset (or investment).
5. LIMITATIONS OF NET PRESENT VALUE (NPV) METHODOLOGY FOR PROJECT ASSESSMENT
So far we have discussed the quantitative part of NPV analysis. Although, it ascertains the return on the investment; still it does not always provide the complete picture required for this kind of decision making. There are other qualitative factors as well that must be considered for in the process.
E.g. investments in research & development or general & administrative areas may not always result in fruitful NPV values. Still these investments are as necessary as any other project for improving the operations & offerings of the company in long run.
Similarly, certain projects must be undertaken by the company just to remain competitive and at par with our competitors; regardless of the capital gains associated with them. For such projects as well, NPV analysis must be avoided.
Other scenarios where NPV analysis might not turn out to be a good option are the projects that involve implementing of new technologies. These projects might require a very significant starting & training costs such that the NPV might almost always result in negative values. Great caution must be employed in determining NPV values for these sort of projects as; these training & implementing costs will provide a base for future developments and thus all of these costs must not be imposed on the very first project itself.