PERPETUITY
Perpetuity refers to the stream of cash flow payments which continues indefinitely. It can also be understood as an annuity that has no end. In valuation analysis, perpetuities are used to find the present value of a company’s future projected cash flow stream and the company’s terminal value.
One of the examples of a perpetuity is in the real-estate sector where an owner purchases a commercial real-estate and then rents it out. The owner is entitled to receive an infinite stream of cash flow as the rent from the property till the property ceases to exist.
Another real-life example is preferred stock, where the perpetuity calculation assumes the company will continue to exist indefinitely in the market and keep paying dividends.
1. PRESENT VALUE (PV) OF PERPETUITY
Present value (PV) of a Perpetuity can be calculated using the below formula:
Where, P = Periodic Payment, r = Rate per period
2. PRESENT VALUE (PV) OF PERPETUITY: DERIVATION
The perpetuity value formula is a simplified version of the present value formula of the indefinite future cash flows received per period. It can be written as follows:
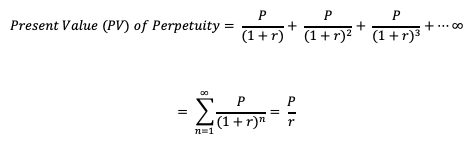
Example. An individual is offered a preferred stock that pays a dividend of $10 per year. It is believed to exist for an infinite period of time. Assuming 5% discount rate, calculate the maximum amount that the investor would be willing to pay for this dividend.
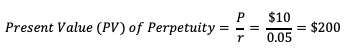
3. PRESENT VALUE (PV) OF A GROWING PERPETUITY
A growing perpetuity is a series of periodic payments that received for an infinite period of time and are growing at a proportionate rate (r).
One of the examples of the growing perpetuity could be commercial real estate where rental cash inflows are expected for an infinite period and will grow over time.
Where P1 = Dividend or Payment in period 1, r = Discount rate; g = Growth rate
4. PRESENT VALUE (PV) OF A GROWING PERPETUITY: DERIVATION
A growing perpetuity is a series of indefinite periodic payments that are growing at a proportionate rate. It can be calculated as follows:
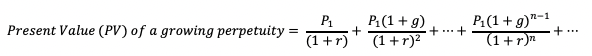
Above equation represents an infinite geometric progression with a common ratio of (1+g)/(1+r). Therefore,

Example. A landlord earns a rental income of $1,0000 per year from his commercial real estate. Expected growth rate for this cash flow is 5% per year and the required rate of return = 10%. Calculate the present value of this growing perpetuity.
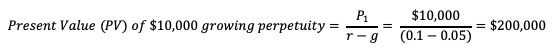
Note: Discount rate (r) must always be higher than the growth rate (g) in the above equation for it to work properly. This is so because present value formula for growing perpetuity is derived using the infinite geometric progression theory and thus if the growth rate becomes higher than the discount rate, the growing perpetuity would have an infinite value.